Solución de sistemas de ecuaciones con el método de Gauss-Jordan en c++

la eliminación de Gauss-Jordanes un algoritmo para determinar las soluciones de un sistema de ecuaciones lineales, encontrar matrices e inversas. Un sistema de ecuaciones se resuelve por el método de Gauss cuando se obtienen sus soluciones mediante la reducción del sistema dado a otro equivalente en el que cada ecuación tiene una incógnita menos que la anterior. El método de Gauss transforma la matriz de coeficientes en una matriz triangular superior. El método de Gauss-Jordan continúa el proceso de transformación hasta obtener una matriz diagonal.

ejemplo:

Supongamos que es necesario encontrar los números "x", "y", "z", que satisfacen simultáneamente estas ecuaciones:

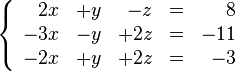
Esto es llamado un sistema de ecuaciones lineales. El objetivo es reducir el sistema a otro equivalente, que tenga las mismas soluciones. Las operaciones (llamadas elementales) son estas:
Multiplicar una ecuación por un escalar no nulo.
Intercambiar de posición dos ecuaciones
Sumar a una ecuación un múltiplo de otra.

Estas operaciones pueden representarse con matrices elementales

En nuestro ejemplo, eliminamos x de la segunda ecuación sumando 3/2 veces la primera ecuación a la segunda y después sumamos la primera ecuación a la tercera. El resultado es:

Ahora eliminamos y de la primera ecuación sumando -2 veces la segunda ecuación a la primera, y sumamos -4 veces la segunda ecuación a la tercera para eliminar y.

Finalmente eliminamos z de la primera ecuación sumando -2 veces la tercera ecuación a la primera, y sumando 1/2 veces la tercera ecuación a la segunda para eliminar z.

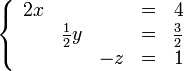
Despejando, podemos ver las soluciones:

Para clarificar los pasos, se trabaja con la matriz aumentada. Podemos ver los 3 pasos en su notación matricial:

Primero:

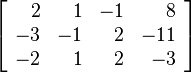
Después,

Por último

.

CÓDIGO EN C++:

#include<iostream>
#include<cmath>
using namespace std;
/*
M-->matriz aumentada
n-->numero de ecuaciones
*/
void gauss_jordan(double M[20][20],int n){
    double may;//variable para almacenar el mayor de la columna k
    int ind;//indice del mayor-->indice de may
    double aux;
    double pivote;
    
    for(int k=0;k<n;k++){//recorrer columnas de la matriz reducida
        may=abs(M[k][k]);
        ind=k;
        //recorrer filas de la columna k para buscar el indice del mayor
        for(int l=k+1;l<n;l++){
            if(may<abs(M[l][k])){
                may=abs(M[l][k]);
                ind=l;
            }
            
        }

        //cambiar filas
        if(k!=ind){
            for(int i=0;i<n+1;i++){
                aux=M[k][i];
                M[k][i]=M[ind][i];
                M[ind][i]=aux;
            }
            
        }
        if(M[k][k]==0){
            cout<<"no tiene solucion";
            break;
        }
        else{
            
            for(int i=0;i<n;i++){//recorrer fila
                if(i!=k){
                    pivote=-M[i][k];
                    for(int j=k;j<n+1;j++){//recorrer elementos de una fila

                        M[i][j]=M[i][j]+pivote*M[k][j]/M[k][k];
                    }
                }
                else{
                    pivote=M[k][k];
                    for(int j=k;j<n+1;j++){
                        M[i][j]=M[i][j]/pivote;
                    }
                }
            }
        }
        
    
}
} 
void ingresar_coeficientes(double M[20][20],int n){
    cout<<"ingrese ecuaciones:"<<endl;
    for(int i=0;i<n;i++){
        cout<<"\t"<<"fila "<<i+1<<" : "<<endl;
        for(int j=0;j<n+1;j++){
            cin>>M[i][j];
        }
    }
}
int main (int argc, char *argv[]) {
    int n;
    double M[20][20];
    cout<<"ingrese numero de ecuaciones:";
    cin>>n;
    ingresar_coeficientes(M,n);
    cout<<"matriz aumentada:"<<endl;
    for(int i=0;i<n;i++){
        for(int j=0;j<n+1;j++){
            cout<<M[i][j]<<"\t";
        }cout<<endl;
    }
    cout<<"reduccion:"<<endl;
    gauss_jordan(M,n);
    for(int i=0;i<n;i++){
        for(int j=0;j<n+1;j++){
            cout<<M[i][j]<<"\t";
        }cout<<endl;
    }
    cout<<"solucion:"<<endl;
    for(int i=0;i<n;i++){
        cout<<"X"<<i+1<<"="<<M[i][n]<<"\t";
    }cout<<endl;
    return 0;
}


Compartir

Unknown