Solución de sistemas de ecuaciones con el método de Gauss-Jordan en c++

la eliminación de Gauss-Jordanes un algoritmo para determinar las soluciones de un sistema de ecuaciones lineales, encontrar matrices e inversas. Un sistema de ecuaciones se resuelve por el método de Gauss cuando se obtienen sus soluciones mediante la reducción del sistema dado a otro equivalente en el que cada ecuación tiene una incógnita menos que la anterior. El método de Gauss transforma la matriz de coeficientes en una matriz triangular superior. El método de Gauss-Jordan continúa el proceso de transformación hasta obtener una matriz diagonal.

ejemplo:

Supongamos que es necesario encontrar los números "x", "y", "z", que satisfacen simultáneamente estas ecuaciones:

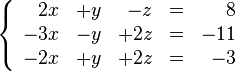
Esto es llamado un sistema de ecuaciones lineales. El objetivo es reducir el sistema a otro equivalente, que tenga las mismas soluciones. Las operaciones (llamadas elementales) son estas:
Multiplicar una ecuación por un escalar no nulo.
Intercambiar de posición dos ecuaciones
Sumar a una ecuación un múltiplo de otra.

Estas operaciones pueden representarse con matrices elementales

En nuestro ejemplo, eliminamos x de la segunda ecuación sumando 3/2 veces la primera ecuación a la segunda y después sumamos la primera ecuación a la tercera. El resultado es:

Ahora eliminamos y de la primera ecuación sumando -2 veces la segunda ecuación a la primera, y sumamos -4 veces la segunda ecuación a la tercera para eliminar y.

Finalmente eliminamos z de la primera ecuación sumando -2 veces la tercera ecuación a la primera, y sumando 1/2 veces la tercera ecuación a la segunda para eliminar z.

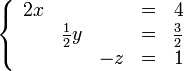
Despejando, podemos ver las soluciones:

Para clarificar los pasos, se trabaja con la matriz aumentada. Podemos ver los 3 pasos en su notación matricial:

Primero:

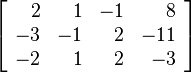
Después,

Por último

.

solución de sistemas de ecuaciones con el método de Gauss(eliminación de Gauss con pivote) en c++

  una técnica que se desarrollo para combatir los     errores de truncamiento por ceros en la diagonal   o los errores de redondeo por números cercanos   a cero es la técnica de pivoteo parcial, esta          técnica consiste en ubicar en la fila pivote el  termino de mayor magnitud de tal forma que al realizar la división por dicho termino no se incurre en la violación de división por números cercanos a cero ni la división por cero.

Se define entonces como:

En cada etapa k se busca el mayor de los elementos de la columna k, que ocupan posiciones mayores o iguales que k, ocupe la posición i, donde k<=i<=n. después se realiza el intercambio de filas. El proceso como tal es idéntico a eliminación gaussiana simple solo que antes de calcular los multiplicadores se realiza el pivoteo si es necesario. Al realizar el pivoteo se obtienen valores lo más pequeños posibles para los multiplicadores reduciendo así el error de redondeo.

Solución de Sistema de ecuaciones con el método de Gauss en c++

el programa que se muestra a continuación
calcula la solución de un sistema de ecuaciones lineales usando el método de la  eliminación de Gauss sin pivote.

calcular el determinante de matriz de cualquier dimensión en c++

en este programa se calcula el determinante de una matriz de cualquier dimensión haciendo uso de la triangularización de una matriz.

Multiplicación De Matrices en c++

  Multiplicación De Matrices usando matrices en c++

Método de bisección en c++

 Este es uno de los métodos más sencillos y de fácil intuición para  resolver ecuaciones en una variable, también conocido como  Método de Intervalo Medio.1 Se basa en el teorema del valor  intermedio (TVI), el cual establece que toda función continua f en  un intervalo cerrado [a,b] toma todos los valores que se hallan  entre f(a) y f(b). Esto es que todo valor entre f(a) y f(b) es la  imagen de al menos un valor en el intervalo [a,b]. En caso de que  f(a) y f(b) tengan signos opuestos, el valor cero sería un valor  intermedio entre f(j) y f(e), por lo que con certeza existe un p en [a,b] que cumple f(p)=0. De esta forma, se asegura la existencia de al menos una solución de la ecuación f(x)=0.

Método de Newton(conocido también como el método de Newton-Raphson o el método de Newton-Fourier) en c++

 En análisis numérico, el método de Newton (conocido también  como el método de Newton-Raphson o el método de Newton-  Fourier) es un algoritmo eficiente para encontrar aproximaciones  de los ceros o raíces de una función real. También puede ser usado  para encontrar el máximo o mínimo de una función, encontrando  los ceros de su primera derivada.

método de falsa posición en c++

 En cálculo numérico, el método de la regula falsi (regla del falso) o  falsa posición es un método iterativo de resolución numérica de  ecuaciones no lineales. El método combina el método de bisección  y el método de la secante.

Rombo de asteriscos en c++

 Escriba un programa que imprima la siguiente figura de rombo. Puede utilizar  instrucciones de salida que imprima un solo asterisco(*) o un solo espacio en  blanco.

Area and perimeter of a rectangle C++ / Área y perímetro de un rectángulo en c++

Write a code in C++ this to find the area and perimeter of a rectangle area = LENGTH * WIDTH . perimeter = 2 * LENGTH + 2 * WIDTH?

SOLUTION:

#include <iostream> 
using namespace std; 
int main (int argc, char *argv[]) { 
    double length ; 
    double width ; 
    double perimeter ; 
    double area; 
    cout<<"Type the width of the rectangle:"; 
    cin>>width; 
    cout<<"Type the length of the rectangle:"; 
    cin>>length; 
    perimeter =2*width+2*length; 
    area=width*length; 
    cout<<"the Area of the rectangle:"<<area<<endl; 
    cout<<"the Perimeter of the rectangle:"<<perimeter<<endl; 
    return 0; 
}

Escriba un código en C++ para encontrar el área y el perímetro de un 
área del rectángulo = largo * ancho 
perímetro = 2 * LONGITUD + 2 * ANCHO

SOLUCIÓN:

#include<iostream>
using namespace std; 
int main (int argc, char *argv[]) { 
    double base; 
    double altura; 
    double perimetro; 
    double area; 
    cout<<"ingrese base del rectangulo:"; 
    cin>>base; 
    cout<<"ingrese altura del rectangulo:"; 
    cin>>altura; 
    perimetro=2*base+2*altura; 
    area=base*altura; 
    cout<<"el area del rectangulo es:"<<area<<endl; 
    cout<<"el perimetro del rectangulo es:"<<perimetro<<endl; 
    return 0; 
}

Conversión de minúscula mayúscula en c++

Conversión de una cadena de caracteres de mayúscula a minúscula sin utilizar funciones predefinidas de c++

Conversión de tipos

Cuando hay diferencia de tipos(int, double, float...) de los operandos en una operación binaria, el compilador los convierte a un tipo común. Existes reglas generales  para estas conversiones aunque varían en algunos compiladores :

1. char, unsigner char, signed char, short, unsigned son convertidos a int, y unsigned short es convertido a unsigned int. Despues de esto, cualquier par de valores asociados con un operador son un int( tambien long y unsigned) , double, float o long double

a partid de este momento, la homogenización de tipos se realiza siguiendo los patrones que se indican( en el orden señalado)

1. Si un operando es de tipo long double, el otro se convertirá a long double.
2. Si un operando es de tipo double, el otro se convertirá a double.
3. Si un operando es de tipo float, el otro se convertirá a float.
4. Si un operando es de tipo unsigned long , el otro se convertirá a unsigned long .
5. Si un operando es de tipo long, el otro se convertirá a long .
6. Si un operando es de tipo unsigned int, el otro se convertirá a unsigned int.
7. Llegados a este punto ambos operandos son int.

veamos ahora el siguiente programa :

#include <iostream> 
using namespace std; 
int main (int argc, char *argv[]) {
    char a='a';
    int b=3;
    float c=3.4f;
    double d=4.78;
    
    
    /*
    ->sin importar que valor tome b, a se convierte en un 97(entero) ya que
    es la posición que ocupa el carácter 'a' en el código ASCII
    ->como b y a ahora son enteros nos dará como resultado de la operación
    un entero
    */
    cout<<a/b<<endl;
    
    /*
    ->sin importar que valor tome b, a se convierte en un 97(entero) ya que
    es la posición que ocupa el carácter 'a' en el código ASCII.
    ->como c es un float a(ahora entero) se convierte en float, por lo tanto
    nos dara un resltado de tipo float
    
    */
    cout<<a/c<<endl;
    
    cout<<c/d<<endl;//c se convierte en un double     
    return 0; 
}
la salida de este programa es:
32
28.5294
0.711297





Ejercicio - Arreglos ,Métodos y Scanner en JAVA

Se  solicita realizar las siguientes operaciones con un Arreglo de 10 posiciones, para cada una de las operaciones programar un método que se llame de un menú principal. 
1. Leer todos los elementos del arreglo 
2. Ordenar de menor a mayor los elementos del arreglo (usar el algoritmo de burbuja) 
3. Imprimir todos los elementos del arreglo 
4. Dado un arregloA de 10 valores y otro arregloB de 10 valores (usar el método de leer arreglo); se debe generar un arregloC, calculado así: 
   -La suma del primer valor del arregloA mas el último valor del arregloB, corresponde al     primer valor del arregloC.      
   -El segundo valor de arregloC será: el segundo valor de arregloA mas el penúltimo de arregloB; y así sucesivamente. 
Finalmente deberán imprimirse los tres arreglos. 
5. Imprimir los números impares que contiene un arreglo 
6. Salir

SOLUCIÓN :

A continuación el código del programa :

package ejercicio1;

import java.util.Scanner;

public class Ejercicio1 {

    private static Scanner ingreso = new Scanner(System.in);

    public static int menu() {
        int opcion = 0;
        String menu = "\n\t MENÚ PRINCIPAL \n"
                + "\n1. Leer Elementos del arreglo."
                + "\n2. Ordenar de forma Ascendente."
                + "\n3. Imprimir arreglo."
                + "\n4. Generar Arreglo C (Suma de Arreglos A y B)"
                + "\n5. Impresion de Números Impares del Arreglo"
                + "\n6. Salir del programa.";
        do {
            System.out.print(menu);
            System.out.print("\nIngrese una opcion: ");
            opcion = ingreso.nextInt();
        } while (opcion < 0 || opcion > 6);
        return opcion;

    }

    private static void LeerArreglo(int[] arreglo) { // Opcion 1

        for (int i = 0; i < 10; i++) {
            System.out.print("Elemento[" + (i + 1) + "]= ");
            arreglo[i] = ingreso.nextInt();
        }

    }

    private static void ImprimirArreglo(int[] arreglo) { // Opcion 3

        for (int i = 0; i < 10; i++) {
            System.out.println("Elemento[" + (i + 1) + "]= " + arreglo[i]);
        }
    }

    public static void OrdenamientoBurbuja(int[] arreglo) { // Opcion 2 - Ascendente
        int aux;
        for (int i = 0; i < arreglo.length - 1; i++) {
            for (int j = 0; j < arreglo.length - i - 1; j++) {
                if (arreglo[j + 1] < arreglo[j]) {
                    aux = arreglo[j + 1];
                    arreglo[j + 1] = arreglo[j];
                    arreglo[j] = aux;
                }
            }
        }
    }

    public static void SumaDeArreglos() { // Opcion 4  
        int[] ArregloA = new int[10];
        int[] ArregloB = new int[10];
        int[] ArregloC = new int[10];
        System.out.println("\nLectura de Elementos [ArregloA]: ...");
        LeerArreglo(ArregloA);
        System.out.println("\nLectura de Elementos [ArregloB]: ...");
        LeerArreglo(ArregloB);

        for (int i = 0; i < 10; i++) {
            ArregloC[i] = ArregloA[i] + ArregloB[10 - i - 1];
        }
        System.out.println("\nImpresión [ArregloC]: ...");
        ImprimirArreglo(ArregloC);
        //Para el primer Caso : ArregloC[0]=ArregloA[0]+ArregloB[9];
        //....................: ArregloC[1]=ArregloA[1]+ArregloB[8];
    }

    public static void NumerosImpares(int[] arreglo) { // Opcion 5 

        for (int i = 0; i < 10; i++) {
            if (arreglo[i] % 2 == 1) {
                System.out.println("Elemento[" + (i + 1) + "]= " + arreglo[i]);
            }
        }
    }

    public static void Return() {
        System.out.print("Presione Enter para Regresar al MENU...");
        new Scanner(System.in).nextLine();
    }

    public static void main(String[] args) {
        int[] Arreglo = new int[10];
        int opt;
        do {
            opt = menu();
            switch (opt) {
                case 1:
                    System.out.println("\nLectura de Elementos: ...");
                    LeerArreglo(Arreglo);
                    Return();
                    break;
                case 2:
                    System.out.println("\nArreglo Ordenado - Imprima Arreglo ...");
                    OrdenamientoBurbuja(Arreglo);
                    Return();
                    break;
                case 3:
                    System.out.println("\nImpresión del Arreglo: ...");
                    ImprimirArreglo(Arreglo);
                    Return();
                    break;
                case 4:
                    System.out.print("\nSuma de Arreglos: ...");
                    SumaDeArreglos();
                    Return();
                    break;
                case 5:
                    System.out.println("\nNúmeros Impares: ...");
                    NumerosImpares(Arreglo);
                    Return();
                    break;
                case 6:
                    System.out.println("Ha cerrado el programa exitosamente . . .");
                    break;
                default:
                    System.err.println("¡ Ha ingresado una opción inválida !");
            }
        } while (opt != 6);
    }
}

Triángulo de Pascal

 Escribir un programa que permita visualizar el triángulo de Pascal:


 En el triángulo de Pascal cada número es la suma de los dos números  situados encima de él.

NÚMERO ARMSTRONG

 elaborar un programa que determine cuántos números son de  ARMSTRONG, desde un "n" hasta un "m". Un número es  ARMSTRONG si la suma de los dígitos elevados a la cantidad de  dígitos que lo componen es igual al número. Ejemplo
 1^3 + 5^3 + 3^3 = 153
 nótese que se eleva al "cubo" porque 153 tiene 3 dígitos. Si fuera  1548 sería a la "cuarta".



SOLUCIÓN:
#include<iostream>
#include<cmath>//utilizar la funciion pow(base,exponente) 
using namespace std; 
int digitos(int x){
    int cont=0;
    while(x>0){
        cont++;
        x=x/10;
    }
    return cont;
} 
int sumaDigitosElevadosCantidadDigitos(int x){
    int cd=digitos(x);//cantidad de digitos     
    int acum=0;//acumulador     
    while(x>0){
        acum=acum+pow(x%10,cd);//el digito elevado al cubo         
        x=x/10;
    }
    return acum;
} 
void numerosARMSTRONG(int n,int m){
    
    for(int i=n;i<=m;i++){
        if(i==sumaDigitosElevadosCantidadDigitos(i))
            cout<<i<<"\t";//mostrar los numeros  ARMSTRONG
    }cout<<endl;//salto de linea
} 
int main (int argc, char *argv[]) {
    int n;
    int m;
    cin>>n;//ingresar valor n     
    cin>>m;//ingresar valor m     
    numerosARMSTRONG(n,m);
    return 0; 
}


Árbol de Navidad

Escribe una función que dado un entero N,
devuelve un árbol de asteriscos de N líneas.

Numero Smith

Diseñar un algoritmo que al ingresar un número, devuelva una "cadena" que indique si el número es Smith o no.
Un número es Smith si la suma de sus dígitos es igual a la suma de los dígitos de cada número de la descomposición canónica.